K近邻法(k-nearest neighbors,KNN)是一种很基本的机器学习方法了，在我们平常的生活中也会不自主的应用。比如，我们判断一个人的人品，只需要观察他来往最密切的几个人的人品好坏就可以得出了。这里就运用了KNN的思想。KNN方法既可以做分类，也可以做回归，这点和决策树算法相同。参考文章

K近邻

K近邻算法，即是给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的K个实例，这K个实例的多数属于某个类，就把该输入实例分类到这个类中。（这就类似于现实生活中少数服从多数的思想）根据这个说法，咱们来看下引自维基百科上的一幅图：

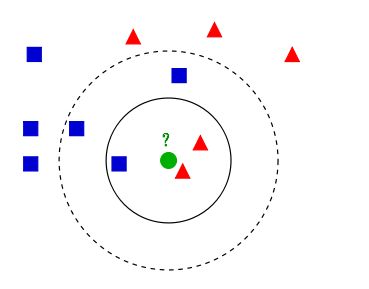
如上图所示，有两类不同的样本数据，分别用蓝色的小正方形和红色的小三角形表示，而图正中间的那个绿色的圆所标示的数据则是待分类的数据。这也就是我们的目的，来了一个新的数据点，我要得到它的类别是什么？好的，下面我们根据k近邻的思想来给绿色圆点进行分类。

如果K=3，绿色圆点的最邻近的3个点是2个红色小三角形和1个蓝色小正方形，少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于红色的三角形一类。

如果K=5，绿色圆点的最邻近的5个邻居是2个红色三角形和3个蓝色的正方形，还是少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于蓝色的正方形一类。

可是在实际问题中，K值的选取是一个问题。我们选取较小的k值，那么就会意味着我们的整体模型会变得复杂，容易发生过拟合！

如果我们选取较大的k值，就相当于用较大邻域中的训练数据进行预测，这时与输入实例较远的（不相似）训练实例也会对预测起作用，使预测发生错误，k值的增大意味着整体模型变得简单。

所以k值的选取，既不能太大，也不能太小，何值为最好，需要实验调整参数确定！

几种度量俩个点之间距离的标准：

1、欧氏距离

2、曼哈顿距离

为了保证每个特征同等重要性，可对每个特征进行归一化

KNN的主要优点有：

　1） 理论成熟，思想简单，既可以用来做分类也可以用来做回归

　2） 可用于非线性分类

　3） 训练时间复杂度比支持向量机之类的算法低，仅为O(n)

　4） 和朴素贝叶斯之类的算法比，对数据没有假设，准确度高，对异常点不敏感

　5） 由于KNN方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合
　
6）该算法比较适用于样本容量比较大的类域的自动分类，而那些样本容量较小的类域采用这种算法比较容易产生误分