数据结构之最小生成树

Share

最小生成树是一副连通加权无向图中一棵权值最小的生成树。

一个连通图可能有多个生成树。当图中的边具有权值时，总会有一个生成树的边的权值之和小于或者等于其它生成树的边的权值之和。

最小生成树算法之Prim算法

Prim算法从任意一个顶点开始，每次选择一个与当前顶点集最近的一个顶点，并将两顶点之间的边加入到树中。Prim算法在找当前最近顶点时使用到了贪婪算法。

算法描述：

1、在一个加权连通图中，顶点集合V，边集合为E

2、任意选出一个点作为初始顶点,标记为visit,计算所有与之相连接的点的距离，选择距离最短的，标记visit.

3、在剩下的点中，计算与已标记visit点距离最小的点，标记visit,加入最小生成树。重复该操作，直到所有点都被标记为visit。

主要来说就是一步一步的寻找离当前点权重最小的点。

详细算法图解：

1、随便从一个点开始，生成最小生成树

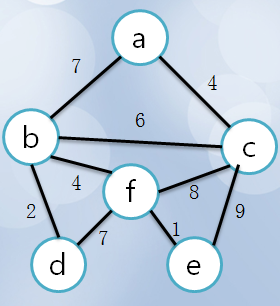
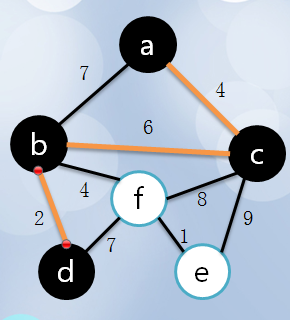
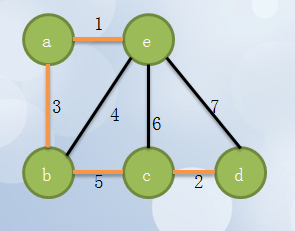
2、假如选择顶点a，顶点a置成visit（涂黑部分）,计算周围与它连接的点的距离

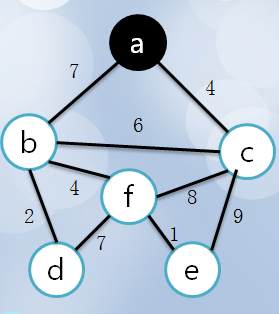
3、与之相连的点距离分别为7,6,4，选择C点距离最短，将C加入所选（visit），同时将这条边加入最小生成树。

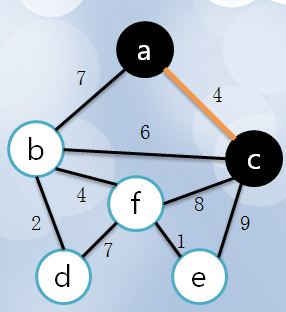
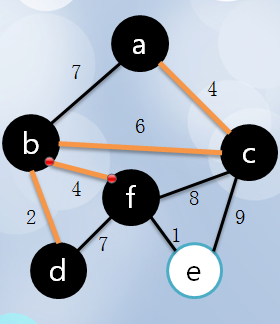
4、现在已选集合中有a,c，选择剩下的点中，离这两个最近的点。分别有7,6,8,9 所以选择6也就是b点加入集合（visit）同时将bc这条边加入最小生成树。

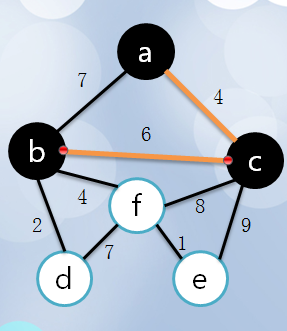
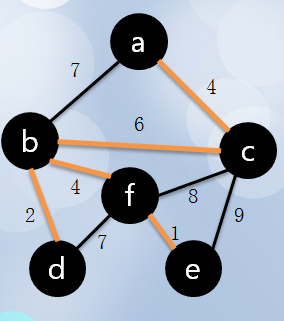
5、重复4，直到所有的点都加入集合（visit），依次所得的即为一颗 最小生成树

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include<iostream>
#define INF 10000
using namespace std;
const int N = 6;
bool visit[N];
int dist[N] = { 0, };
int graph[N][N] = { {INF,7,4,INF,INF,INF},   //INF代表两点之间不可达
                    {7,INF,6,2,INF,4}, 
                    {4,6,INF,INF,9,8}, 
                    {INF,2,INF,INF,INF,7}, 
                    {INF,INF,9,INF,INF,1}, 
                    {INF,4,8,7,1,INF}
                  };
int prim(int cur)
{
    int index = cur;
    int sum = 0;
    int i = 0;
    int j = 0;
    cout << index << " ";
    memset(visit, false, sizeof(visit));
    visit[cur] = true;
    for (i = 0; i < N; i++)
        dist[i] = graph[cur][i];//初始化，每个与a邻接的点的距离存入dist
    for (i = 1; i < N; i++)
    {
        int minor = INF;
        for (j = 0; j < N; j++)
        {
            if (!visit[j] && dist[j] < minor)          //找到未访问的点中，距离当前最小生成树距离最小的点
            {
                minor = dist[j];
                index = j;
            }
        }
        visit[index] = true;
        cout << index << " ";
        sum += minor;
        for (j = 0; j < N; j++)
        {
            if (!visit[j] && dist[j]>graph[index][j])      //执行更新，如果点距离当前点的距离更近，就更新dist
            {
                dist[j] = graph[index][j];
            }
        }
    }
    cout << endl;
    return sum;               //返回最小生成树的总路径值
}
int main()
{
    cout << prim(0) << endl;//从顶点a开始
    return 0;
}

最小生成树算法之Kruskal

如果说prime算法是对点的选择，那么Kruskal算法可以说是对于边的选择。

每一次选择权重最小的边，判断其顶点是否已存在集合中，若无则将其加入集合。（特别注意：不能连成环！）

图解：

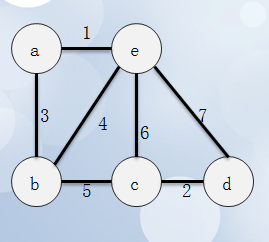
1、取出最小边，也就是将a,e放入同一个集合

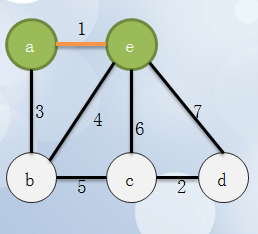
2、接着寻找最小边，也就是将c,d加入同一个集合

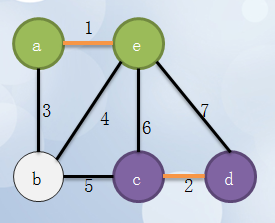
3、重复寻找

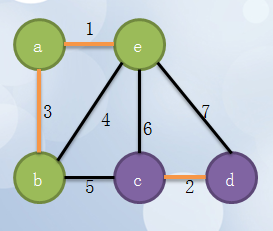
4、因为b,e都属于同一个集合了，会构成环。所以不能选择be这条边!

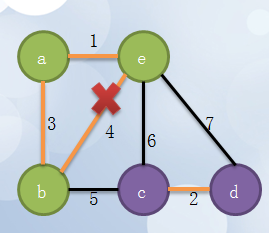
5、再找到bc，因为不属于同一个集合，所以合并这两个集合。所有的点都选择完毕，生成最小生成树。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
#include<iostream>
#define N 7
using namespace std;
typedef struct _node{
    int val;
    int start;
    int end;
}Node;
Node V[N];
int cmp(const void *a, const void *b)
{
    return (*(Node *)a).val - (*(Node*)b).val;
}
int edge[N][3] = {  { 0, 1, 3 },
                    { 0, 4, 1 }, 
                    { 1, 2, 5 }, 
                    { 1, 4, 4 },
                    { 2, 3, 2 }, 
                    { 2, 4, 6 }, 
                    { 3, 4, 7} 
                    };

int father[N] = { 0, };
int cap[N] = {0,};

void make_set()              //初始化集合，让所有的点都各成一个集合，每个集合都只包含自己
{
    for (int i = 0; i < N; i++)
    {
        father[i] = i;
        cap[i] = 1;
    }
}

int find_set(int x)              //判断一个点属于哪个集合，点如果都有着共同的祖先结点，就可以说他们属于一个集合
{
    if (x != father[x])
     {                              
        father[x] = find_set(father[x]);
    }     
    return father[x];
}                                  

void Union(int x, int y)         //将x,y合并到同一个集合
{
    x = find_set(x);
    y = find_set(y);
    if (x == y)
        return;
    if (cap[x] < cap[y])
        father[x] = find_set(y);
    else
    {
        if (cap[x] == cap[y])
            cap[x]++;
        father[y] = find_set(x);
    }
}

int Kruskal(int n)
{
    int sum = 0;
    make_set();
    for (int i = 0; i < N; i++)//将边的顺序按从小到大取出来
    {
        if (find_set(V[i].start) != find_set(V[i].end))     //如果改变的两个顶点还不在一个集合中，就并到一个集合里，生成树的长度加上这条边的长度
        {
            Union(V[i].start, V[i].end);  //合并两个顶点到一个集合
            sum += V[i].val;
        }
    }
    return sum;
}
int main()
{
    for (int i = 0; i < N; i++)   //初始化边的数据，在实际应用中可根据具体情况转换并且读取数据,这边只是测试用例
    {
        V[i].start = edge[i][0];
        V[i].end = edge[i][1];
        V[i].val = edge[i][2];
    }
    qsort(V, N, sizeof(V[0]), cmp);
    cout << Kruskal(0)<<endl;
    return 0;
}

ps:代码与图解来自网页