动态规划,对于子问题重叠的情况特别有效,因为它将子问题的解保存在表格中,当需要某个子问题的解时,直接取值即可,从而避免重复计算。
- 适用情况
(a) 最优化原理:如果问题的最优解所包含的子问题的解也是最优的,就称该问题具有最优子结构,即满足最优化原理。
(b) 无后效性:即某阶段状态(定义的新子问题)一旦确定,就不受这个状态以后决策的影响。也就是说,某状态以后的过程不会影响以前的状态,只与其以前的状态有关。
(c)有重叠子问题:即子问题之间是不独立的(分治法是独立的),一个子问题在下一阶段决策中可能被多次使用到。(该性质并不是动态规划适用的必要条件,但是如果没有这条性质,动态规划算法同其他算法相比就不具备优势)
- 求解步骤
(1)分析最优解的性质,并刻画其结构特征,这一步的开始时一定要从子问题入手。
(2)定义最优解变量,定义递归最优解公式。
(3)以自底向上计算出最优值(或自顶向下的记忆化方式(即备忘录法))
(4)根据计算最优值时得到的信息,构造问题的最优解
例子: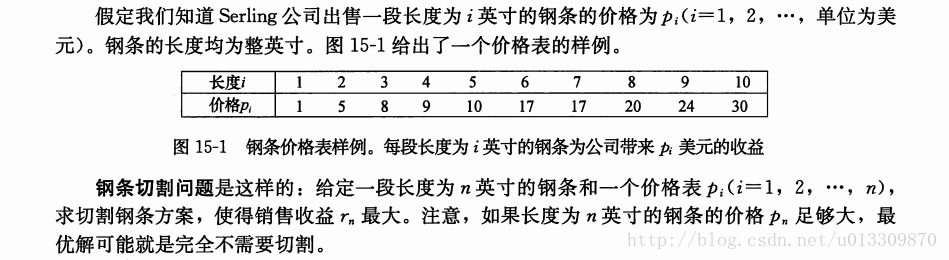
使用动态规划求解:
1、带备忘录的自顶向下方法:保存每一个子问题的解,求解时首先检查是否已经保存过,如果是,则直接返回保存的值;否则,计算该值。
2、自底向上法:
求解子问题时,其需要的子子问题都已经求解完毕。
带备忘录的自顶向下方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <iostream>
#include<vector>
using namespace std;
int cut(int *p,int n,int *r)
{
int q;
if(r[n]>=0)
{
return r[n];
}
if(n==0)
{
q=0;
}
else
{
q=-999;
for(int i=1;i<=n;i++)
{
q=max(q,p[i]+cut(p,n-i,r));
}
}
r[n] = q;
return q;
}
int main()
{
int p[]={0,1,5,8,9,10,17,17,20,24,30};
int r[11];
for (int i=0;i<=10;i++)
{
r[i] = -999;
}
int n = 7;
cout<<cut(p,n,r)<<endl;
for (int i=1;i<=10;i++)
{
cout<<r[i]<<" ";
}
}自底向上法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
int bottom_up_cut(int *r,int *p,int n)
{
for(int j=1;j<=n;j++)
{
int q= -999;
for(int i=1;i<=j;i++)
{
q = max(q,p[i]+r[j-i]);
}
r[j]=q;
}
return r[n];
}
int main()
{
int p[]={0,1,5,8,9,10,17,17,20,24,30};
int r[11];
for (int i=0;i<=10;i++)
{
r[i] = 0;
}
int n = 7;
cout<<bottom_up_cut(r,p,n)<<endl;
for (int i=1;i<=10;i++)
{
cout<<r[i]<<" ";
}
}