定义
贪心算法是指在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,只做出在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择,选择的贪心策略必须具备无后效性,即某个状态以前的过程不会影响以后的状态,只与当前状态有关。
关键点:
- 局部最优解
- 满足最优子问题结构
最常见的例子就是找零钱问题了:
用动态规划解答的话,表达式可以这样写出: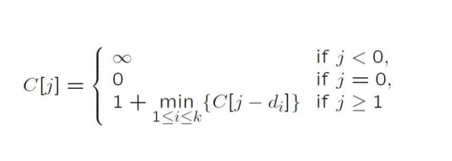
例如: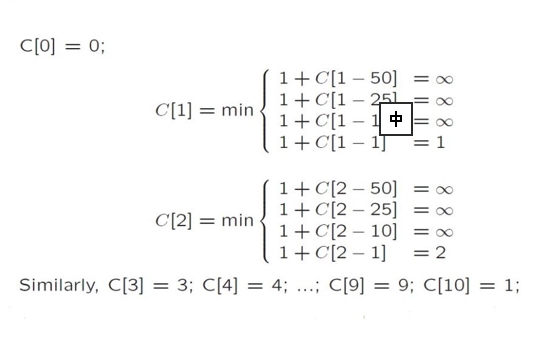
1 | n = 15 |
但是这个的缺点就是对于每一种情况都会去遍历,当数量很大时浪费空间。
用贪心算法:
每一次都选择小于等于所找面额中的最大硬币值:` bash
#例如:
n = 58
d = [1,5,10,50,100]
C = [999 for i in range(n+1)]
denom = []
#denom = [0 for i in range(n+1)] #找钱的方法
def compute_change(n,d):
while(n>0):
for i in range(len(d)):
if(n>=d[i]):
continue
denom.append(d[i-1])
break
n = n-d[i-1]
print denom
compute_change(n,d)
···
对于经典的背包问题:在选择物品i装入背包时,可以选择物品的一部分,而不一定要全部装入背包。这种情况就可以使用贪心算法求解。计算每种物品的单位重量价值作为贪心选择的依据指标,选择单位重量价值最高的物品,将尽可能多的该物品装入背包,依此策略一直地进行下去,直到背包装满为止。
- 在零一背包问题中贪心选择之所以不能得到最优解原因是贪心选择无法保证最终能将背包装满,部分闲置的背包空间使每公斤背包空间的价值降低了。
对于贪心算法,经典的例子还有活动选择问题

1.具有最优子结构
2.贪心选择

伪代码: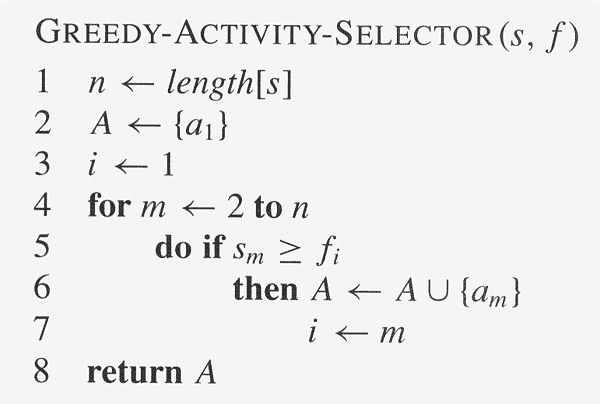
贪心算法到此为止,接下来继续复习动态规划……